FUNCIONAMIEMTO FRV

Tabla de versiones

Release	Description	Date	By	Aproved
0.1	Well FRV design	19/02/20	HG

Objective and scope

Background

E- VRF downhole valves for water injection in oil wells fullfil the function to deliver water at the necessary pressure and flow at each level of the well’s rock formation. Once selected the VRF according to the criteria indicated by the provider and the hydraulic flow analyzes the injection into each zone should be flow regulated and constant.

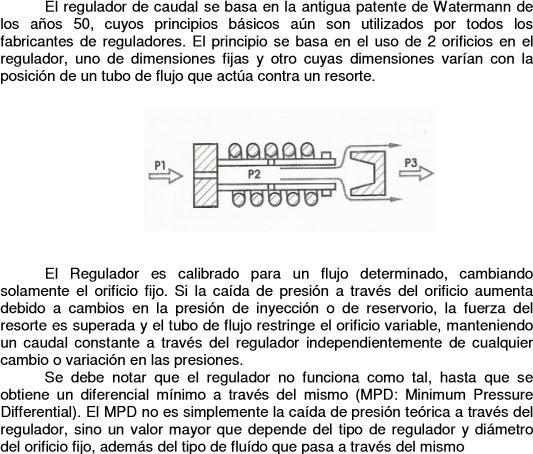
Watermann FRV Valve

These ideal conditions are not present in all cases, which makes it necessary to remove «Strings» and change the corresponding valve.

On the other hand there are new injection techniques that include the use of a mix of water and polymer. In this last option needs to avoid shear degradation of the polymer. In this way the valve has to produce the minimal shear rate when the fluid is passing trouhg it.

S- Las válvulas de fondo de pozo VRF para inyección de agua en pozos de petróleo cumplen la función de entregar agua a la presión y caudal necesarios en cada uno de los niveles de la formación rocosa del pozo. Una vez seleccionadas las VRF de acuerdo con los criterios indicados por el proveedor de las mismas y los análisis hidráulicos, se espera que los caudales inyectados en cada una de las zonas estén regulados y tengan flujo constante. Estas condiciones ideales no se presentan en todos los casos, lo que hace necesario retirar «Sartas» y cambiar las correspondientes válvula.

Por otra parte, hay nuevas técnicas de inyección que incluyen el uso de una mezcla de agua y polímero. Para esta opción se require evitar la degradación por cortante del polímero. Para esto es necesario que durante el flujo a través de la válvula se minimicen los esfuerzos cortantes.

Objective

E- It is required:

• Verify that the hydraulic losses in the main elements of the Wellbore match the data indicated for existing models.

• To design a FRV valve that meets the neccesary conditions.

• Design a new water-polymer valve model that allows the injection without degrade the polymer.

S- Se requiere:

• Verificar que las pérdidas hidráulicas en los elementos principales del Wellbore correspondan con los datos indicados para modelos existentes y diseñar un modelo de válvula que pueda mejorar las condiciones de inyección.

• Diseñar un modelo de válvula que permita la inyección de agua con polímero sin degradar este último.

Specific objectives

E-

• Verify the operation curves (Flow vs. Pressure) of the FRV valves currently used for control of the flow injected into each of the well zones.

• Calculate the hydraulic losses in VRFs.

• Verify or find differences with what is indicated by the supplier of the analyzed elements.

• Extrapolation of what was obtained in the dynamic model of current valves through analytical calculation for different hole diameters.

• Identify possible points of improvement for the operation of well injection valves.

• Identify the correct parameters required in the operation of the valves.

• Design new valves for the purposes indicated above.

S-

• Verificar las curvas de operación (Caudal vs. Presión) de las válvulas FRV utilizadas actualmente para el control del caudal inyectado a cada una de las zonas de los pozos.

• Calcular las pérdidas hidráulicas en VRFs.

• Verificar o encontrar diferencias con lo indicado por proveedor de los elementos analizados.

• Extrapolación de lo obtenido en el modelo dinámico de válvulas actuales mediante cálculo anlítico para diferentes diámetros de agujero.

• Identificar posible puntos de mejora de la operación de válvulas de fondo de pozo.

• Identificar los parámetros correctos requeridos en la operación de las válvulas.

• Diseñar nuevas válvulas para los propósitos arriba indicados.

Scope

E- Empirical data and analytical equations are used to approximate the pressure drops of the elements to study and / or to calibrate the models.

Axisymmetric models of the main parts of the valve are made, corresponding to those with axial symmetry. The pressure drops of the inlet and outlet as they are not axisymmetric will be analytically modeled.

The K constants of losses and flow curves against pressure of the VRF are presented in a tabular way.

S- Se utilizan datos empíricos y ecuaciones analíticas para aproximar las caidas de presión de los elementos a estudiar y/ó para calibrar los modelos.

Se realizan modelos axisimétrico de las partes principales de la válvula, correspondientes a las que tienen simetría axial. Las caidas de presión de la entrada y salida por no ser axisimétricas se modelarán analiticamente.

Se entregan de manera tabular las constantes K de pérdidas y curvas de caudal contra presión de las VRF.

Summary

Activities

E-

• The behavior of the valves in the open position was simulated to determine the initial pressure drop of them before starting the regulation.

S-

• Se simuló el comportamieto de las válvulas en posición abierta para determinar la caida de presión inicial de las mismas antes de iniciar la regulación.

Preliminary

E-

An evaluated existing model of valves promises to control flow by a curve.

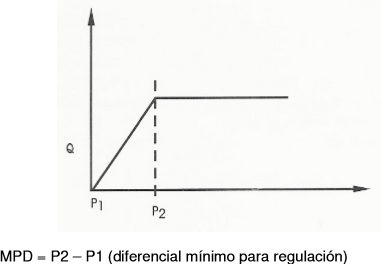
Flow vs. Pressure curve FRV Valve

Where P2 should correspond to the Delta P values shown in the next table.

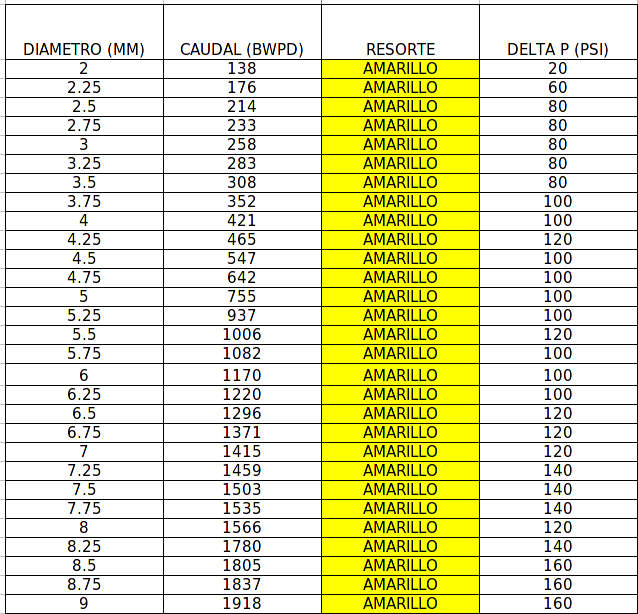
P2-Pressure drop in function of flow and hole diameter - Vendor promised.

It was made an initial calculation that shows the teorical P2 for the hole and the flow. Itś possible to see that the P2 couldn’t be the promised in the previous table.

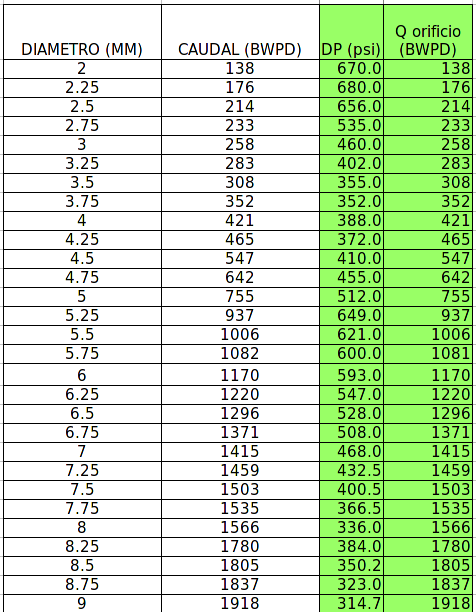
P2-Pressure drop in function of flow and hole diameter - Calculated.

The previos calculation was made by:

Pressure drop calculation through a hole.

And:

Pressure drop calculation through a hole - Crane.

The dischargue coefficient used is of 0,7.

Concluding, the Vendor promised values for P2 are physically impossible. The consequences for the cusomers is that the hydraulic calculations and pressure supplys should be different than the used with the Vendor informed values.

In order to verify the previous results there where developed static and dynamic CFD (Computer Fluid Dynamics) models.

Static model

Coeficiente CV de pérdidas y caida de presión de las VRF según diámetro de entrada válvula abierta, antes de iniciar regulación.

Hole Diameter [mm]	simulated Cv	Operation Flow [BWPD]	Pressure drop [psi]
2		138
2.25		176
2.5		214
2.75		233
3		258	432
3.25		283
3.5		308
3.75		352
4		421
4.25		465
4.5		547
4.75		642
5		755
5.25		937
5.5		1006
5.75		1082
6		1170
6.25		1220
6.5		1296
6.75		1371
7		1415
7.25		1459
7.5		1503
7.75		1535
8		1566
8.25		1780
8.5		1805
8.75		1837
9		1918

Coeficiente K de pérdidas en Slleve SCH-80 y caida de presión a la velocidad media de trabajo de las lineas del cliente.

Slleve	k	Velocidad de trabajo [ft/s]	Caída de presión [psi]
3» SCH-80	0.7	7	0.23
4» SCH-80	0.435	7	0.144
6» SCH-80	0.297	7	0.098
8» SCH-80	0.21	7	0.07
10» SCH-80	0.15	7	0.05
12» SCH-80	0.112	7	0.037

Para ser usado mediante la relación (unidades sistema Internacional):

\[h_{f} = K \frac{v^2}{2 g}\]

Recomendaciones

• Se recomienda utilizar los resultados aquí calculados para determinar pérdidas de caida de presión en las tuberías.

Unidades

Unidades principales en el sistema internacional

Longitud:	\(m\)
Masa:	\(kg\)
Fuerza:	\(N\)
Tiempo:	\(s\)
Presión:	\(pa\)
Densidad	\(\frac{kg}{m^3}\)
Viscosidad dinámica	\(pa s\)
Viscosidad cinemática	\(\frac{m^2}{s}\)
Coeficiente de Presión openFoam	\(\frac{m^2}{s^2}\)
Velocidad	\(\frac{m}{s}\)

Unidades utilizadas en otros sistemas de unidades

Temperatura	\(F\)
Viscosidad dinámina en centiPoises	\(cP\)
Presión psi	\(psi\)
Velocidad ft/s	\(\frac{ft}{s}\)

Geometría

La información con la geometría de los slleves fue suministrada por el cliente en el plano: GATH-LCI-407-95-23-065.dwg cuyo contenido se ve en las siguientes figuras.

Se observa que el modelo corresponde al Slleve y dos tramos de tubo, uno a la entrada y otro a la salida. Los tramos de tubería tienen longitud de 10 diámetros cada uno. De esta manera que se eliminan efectos transitorios y errores numéricos que podrían ocurrir cerca de la entrada y la salida del modelo.

Construcción del modelo

Fluidos

Fluido de baja presión

El fluido transportado .

Malla

La malla de elementos finitos construida para el modelo se realizó mediante

La figura siguiente muestra las características de la malla elaborada.

Condiciones de frontera

El modelo realizado requiere de condiciones de frontera y condiciones iniciales consistentes para su funcionamiento. Las siguientes son las condiciones aplicadas al modelo.

Condiciones de velocidad

• Entrada del fluido: Se modela la velocidad de entrada correspondiente al máximo valor de diseño (8 \(\frac{ft}{s}\) para el fluido multifásico y 10 \(\frac{ft}{s}\) para el fluido de inyección).

• Velocidad inicial: Se modela con el mismo valor del de la entrada del fluido.

• Velocidad en las paredes: Se modela con velocidad cero en la pared (no slip).

Condiciones de presión

• Salida del fluido: Se coloca a la salida la presión máxima de trabajo.

• Entrada del fluido: Esta presión será cálculada y es el valor de salida esperado.

• Paredes: condición de zero gradiente.

• En el software utilizado (openFoam 5.x) se requiere cómo dato de presión la cantidad:

\[P*_{of}=\rho p\]

• Del mismo modo la presión obtenida debe dividirse entra la densidad para obtener el valor en unidades consistentes (\(pa\) este caso).

Condiciones de turbulencia

• Entrada salida y paredes: Se calcula valor de \(\kappa\) y \(\epsilon\) de acuerdo con las condiciones de flujo (Reynolds), y se asignan valores iniciales al modelo en la entrada, salida, pared y volumen.

Corrida y postprocesamiento

Los modelos se cargaron de acuerdo con lo indicado lineas arriba en el numeral correspondiente a las cargas y se corrieron con el software de elementos seleccionado (Ver numeral Software).

Se obtuvieron resultados de caida de presión y velocidades a través de los Slleves como se ilustra a continuación.

Software

Para la elaboración de este proyecto se utilizó el software de volúmenes finitos openFoam 5.x.

Hardware y tiempo de corrida

Para la ejecución de los modelos se utilizó un equipo con procesador Core i7 de 8va generación, 32GB Ram, con tiempos de corrida promedio de 10.000 segundos con un procesador y/o 3.000segundos con 12 procesadores.

Cálculo SCH-STD

Resultados

En la tabla siguiente se resumen los resultados obtenidos para la caida de presión enlos Slleves que utiliza actualmente el cliente.

Resultados de caida de presión en Slleves SCH-STD, a las velocidades mínima y máxima de diseño

Sllleve	Velocidad del fluido [\(\frac{ft}{s}\)]	Caida de presión [\(psi\)]
3» SCH-STD	8	0.27
	3	0.037 [4]
6» SCH-STD	8	0.128
	3	0.019 [4]
16» SCH-STD	8	0.035
	3	0.0049 [4]

[4] (1,2,3)

Este valor no se modeló, en cambio se calculó usando la relación de caudal al cuadrado para pérdidas.

Cálculo SCH-80

Resultados de caida de presión en Slleves SCH-80, a las velocidades mínima y máxima de diseño

Sllleve	Velocidad del fluido [\(\frac{ft}{s}\)]	Caida de presión [\(psi\)]
3» SCH-80	10	0.36
	3	0.032 [5]
12» SCH-80	10	0.076
	3	0.007 [5]

[5] (1,2)

Este valor no se modeló, en cambio se calculó usando la relación de caudal al cuadrado para pérdidas.

Verificaciones

Efecto del tamaño de la malla

Se realizaron pruebas para encontrar la influencia del tamaño de la malla en el error de cálculo para la caida de presuión. Se utilizó para este efecto el modelo del Slleve de 3» SCH-STD con los siguientes resultados.

Caida de presión para diferentes tamaños de malla

Número de volúmenes	Caida de presión calculada [\(psi\)]
270.000	7.345
640000	2.160
1’250.000	0.650
2’400.000	0.27

En la figura siguiente se grafica el efecto del tamaño de la malla en la precisión del cálculo de la caida de presión. Con base en este resultado se define que el tamaño de malla para la elaboración de los modelos será cómo mínimo de 1’250.000 volúmenes finitos.

Si bien los valores del tamaño de la malla no son determinantes para la convergencia porque después del cálculo inicial se requieren algunos parámetros adicionales, la escogencia de una buena malla permitirá mejorar la precisión del cálculo.

Cálculo analítico

Para el cálculo analítico de las pérdidas por fricción se consideran una contracción y una expansión bruscas.

Para el sistema de agua de inyección se utiliza la relación:

\[h= \sum{K} \frac{v^2} {2 g}\]

Para el cálculo del K de perdidas para la reducción se utiliza la ecuación (2) de la bibliografía [6]

\[K_{BR} = 0.50926435 - 0.28767429 \frac{A_{2}}{A_{1}} - 1.4840581 (\frac{A_{2}}{A_{1}})^2.^5 + 1.2643591 (\frac{A_{2}}{A_{1}})^3\]

Para la expansión el K de pérdidas se calcula con la ecuación (25) de la bibliografia [6]

\[K_{AB} = 0.99906174 + 0.13856654 (\frac{A_{2}}{A_{3}})^0.^5 - 2.4035102 (\frac{A_{2}}{A_{3}}) + 1.6373483 (\frac{A_{2}}{A_{3}})^2 - 0.37144824 (\frac{A_{2}}{A_{3}})\]

Con:

\(A_{1}\) Area del tubo antes de la reducción [\(m\)] \(A_{2}\) Area del diametro interno del Slleve [\(m\)] \(A_{3}\) Area del tubo despues de la expansión [\(m\)]

Usando estas ecuaciones se realizaron los cálculos de la siguiente tabla.

Cálculo de la caida de presión mediante los coeficientes K

Sllleve	Velocidad del fluido [\(\frac{ft}{s}\)]	\(k_{BR}\)	\(k_{AB}\)	Caida de presión Calculada [\(psi\)]	Caida de presión modelada [\(psi\)]	Diferencia [%]
3» SCH-80	10	0.298	0.3161	0.41	0.36	13.8
12» SCH-80	10	0.075	0.056	0.088	0.112	21
3» SCH-STD	8	0.273	0.28	0.23	0.27	14.8
6» SCH-STD	10	0.14	0.11	0.108	0.128	15.6
16» SCH-STD	10	0.048	0.036	0.036	0.034	5.88

[6] (1,2)

Expresiones analíticas del coeficiente de pérdidas de energía en dispositivos de reducción del diámetro bajo régimen forzado, JoséJ.Villegas-León, Alvaro López-Lambraño, JoséG.Morales-Nava, Máximo Pliego-Díaz, Carlos Fuentes, Alvaro López-Ramos, 2015

Límites del análisis

• Los análisis corresponden a la solución de la ecuación de Navier Stokes para flujo estacionario.

• Los valores de caida de presión cálculados son numericamente pequeños con respecto a los valores de referencia (presiones de diseño), esto genera inestabilidades numéricas que debieron revisarse cuidadosamente para obtener convergencia.

Anexos

• Gráficas de resultados
  • Esfuerzos en Slleves actuales