CAIDA DE PRESIÓN EN SLLEVES

Tabla de versiones

Release	Descripción	Fecha	Elaboró	Aprobó
0.1	Se envió para revisión del cliente	10/09/19	HG

Objetivo y alcance

Objetivo

Verificar caída de presión del fluido pasando por los Sleeves utilizados por el cliente en las tuberías de SCH-STD y SCH-80.

Alcance

Se hicieron modelos de flujo a través de los Sleeves y se calculó la caída de presión del fluido debida al paso a través de estos elementos. Esta información complementará el conocimiento del cliente acerca de las perdidas a utilizar en su modelamiento de tuberías.

Resumen

Actividades

• Se modelaron los Slleves para tuberías SCH-STD y SCH-80 y se calculó la caida de presión a través de estos para las velocidades máxima y mínima de diseño.

• Se compararon los resultados con la relación empírica usada para el cálculo de la caida de presión a través de una contracción y expansión bruscas en serie. Este cálculo permitió la validación de los órdenes de magnitud de los resultados.

• Se realizó interpolación con base en los resultados obtenidos y se produjo una tabla de K de pérdidas para todos los diámetros de Slleves que están dentro del rango de la simulación.

• Los valores de K de pérdidas a utilizar en los Slleve modelados son los siguientes:

Coeficiente K de pérdidas en Slleve SCH-STD y caida de presión a la velocidad media de trabajo de las lineas del cliente.

Slleve	k	Velocidad de trabajo [ft/s]	Caída de presión [psi]
3» SCH-STD	0.47	5	0.079
4» SCH-STD	0.36	5	0.06
6» SCH-STD	0.21	5	0.035
8» SCH-STD	0.11	5	0.018
10» SCH-STD	0.10	5	0.017
12» SCH-STD	0.098	5	0.016
14» SCH-STD	0.094	5	0.0157
14» SCH-40	0.097	5	0.0162
16» SCH-STD	0.0889	5	0.0148

Coeficiente K de pérdidas en Slleve SCH-80 y caida de presión a la velocidad media de trabajo de las lineas del cliente.

Slleve	k	Velocidad de trabajo [ft/s]	Caída de presión [psi]
3» SCH-80	0.7	7	0.23
4» SCH-80	0.435	7	0.144
6» SCH-80	0.297	7	0.098
8» SCH-80	0.21	7	0.07
10» SCH-80	0.15	7	0.05
12» SCH-80	0.112	7	0.037

Para ser usado mediante la relación (unidades sistema Internacional):

\[h_{f} = K \frac{v^2}{2 g}\]

Recomendaciones

• Se recomienda utilizar los resultados aquí calculados para determinar pérdidas de caida de presión en las tuberías.

Unidades

Unidades principales en el sistema internacional

Longitud:	\(m\)
Masa:	\(kg\)
Fuerza:	\(N\)
Tiempo:	\(s\)
Presión:	\(pa\)
Densidad	\(\frac{kg}{m^3}\)
Viscosidad dinámica	\(pa s\)
Viscosidad cinemática	\(\frac{m^2}{s}\)
Coeficiente de Presión openFoam	\(\frac{m^2}{s^2}\)
Velocidad	\(\frac{m}{s}\)

Unidades utilizadas en otros sistemas de unidades

Temperatura	\(F\)
Viscosidad dinámina en centiPoises	\(cP\)
Presión psi	\(psi\)
Velocidad ft/s	\(\frac{ft}{s}\)

Geometría

La información con la geometría de los slleves fue suministrada por el cliente en el plano: GATH-LCI-407-95-23-065.dwg cuyo contenido se ve en las siguientes figuras.

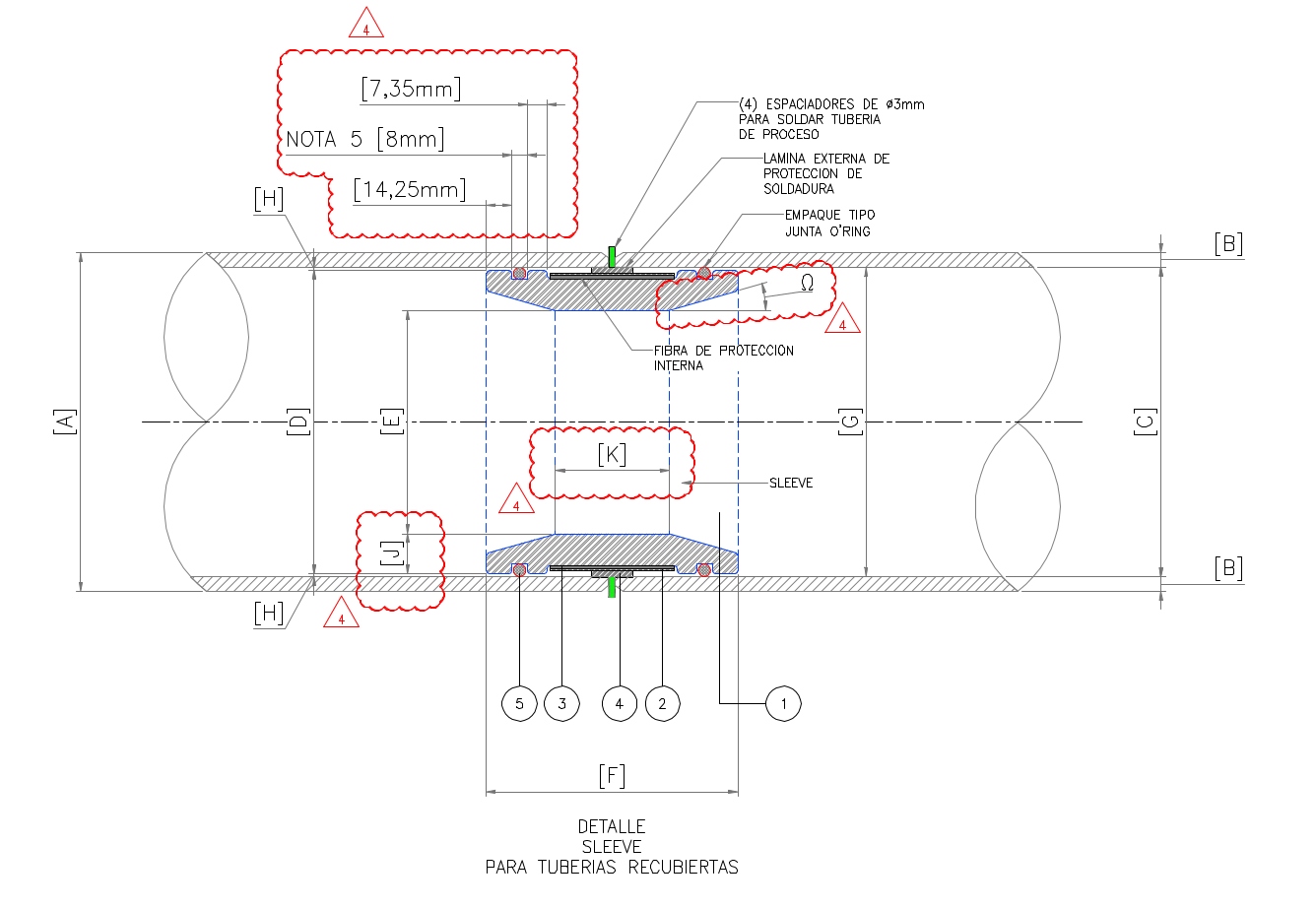
Geometría.

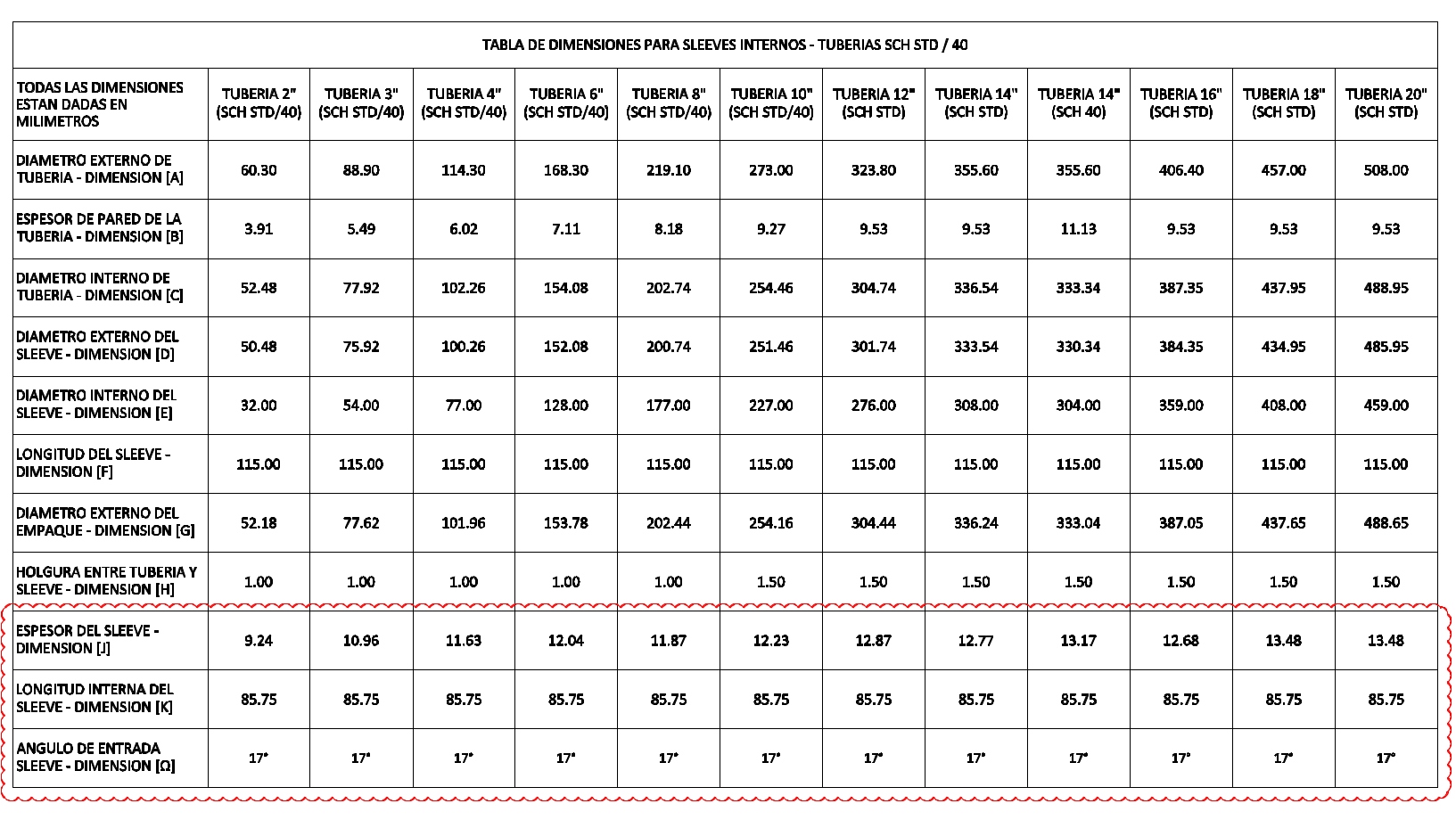
Dimensiones SCH-STD.

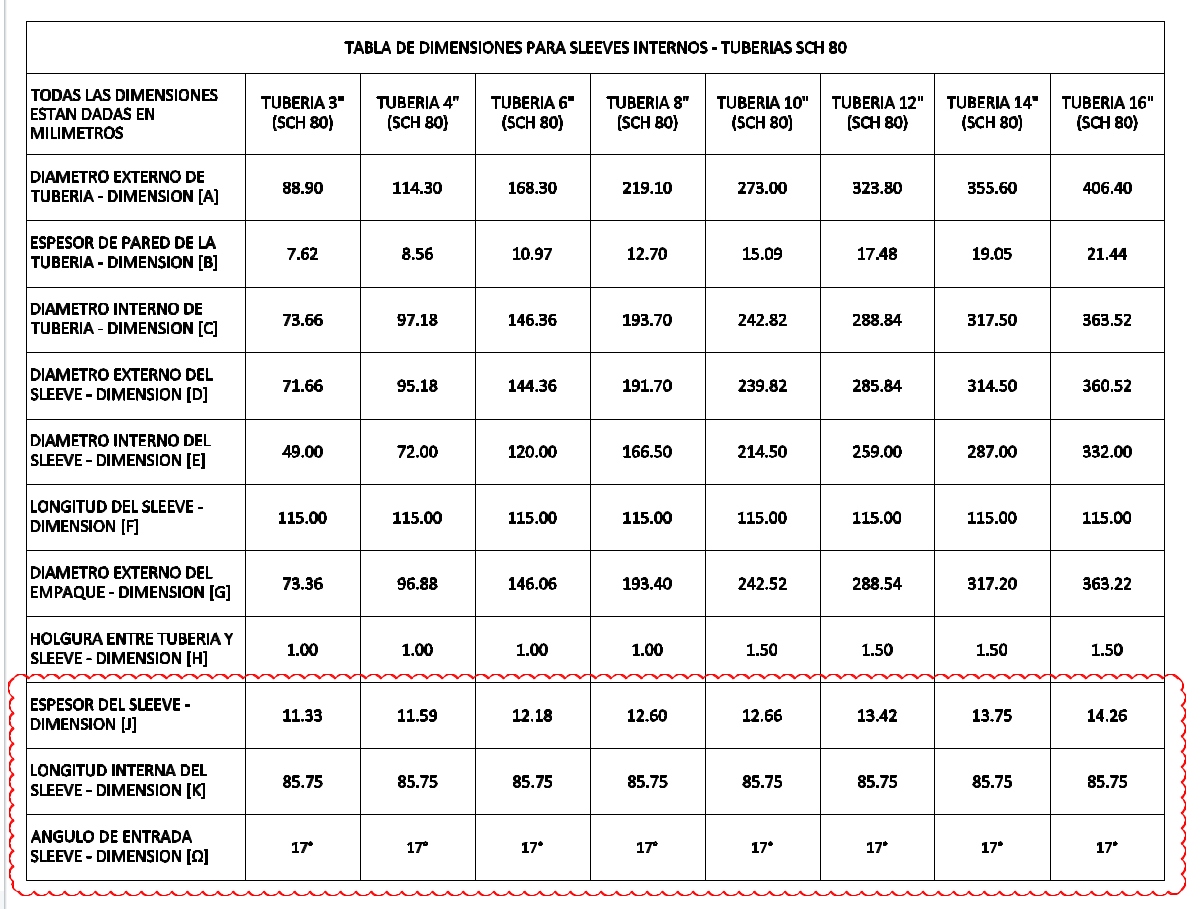
Dimensiones SCH-80.

Se observa que el modelo corresponde al Slleve y dos tramos de tubo, uno a la entrada y otro a la salida. Los tramos de tubería tienen longitud de 10 diámetros cada uno. De esta manera que se eliminan efectos transitorios y errores numéricos que podrían ocurrir cerca de la entrada y la salida del modelo.

Construcción del modelo

Fluidos

Fluido de baja presión

El fluido transportado por la tubería de SCH-STD de este estudio, es una mezcla de agua, crudo de 25 grados API y gas.

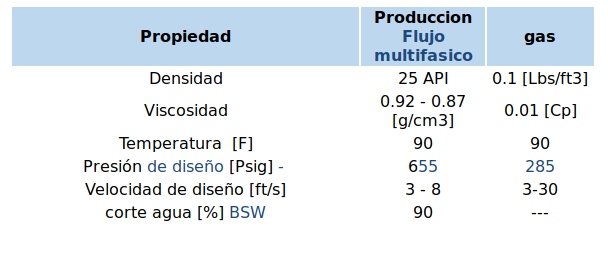
Propiedades del fluido de baja presión

En la tabla siguiente se presentan los datos de entrada para calcular las propiedades de la mezcla:

Propiedades utilizadas para el cálculo

Fluido	Propiedad	Valor
Agua	Temperatura	90.0 \(F\)
	Presión	655 \(psi\)
	BSW	90
	Densidad	1003 \(\frac{kg}{m^3}\)
	Viscosodad dinámica	0.7599 \(cP\)
Crudo	Temperatura	90.0 \(F\)
	Presión	655 \(psi\)
	BSW	90
	Densidad	900 \(\frac{kg}{m^3}\)
	Viscosodad dinámica	180.2 \(cP\)
Gas	Temperatura	90.0 \(F\)
	Presión	655 \(psi\)
	%w	0.16
	Densidad	0.388 \(\frac{kg}{m^3}\)
	Viscosodad dinámica	0.01 \(cP\)

Con esta información se calculó la densidad media cómo el promedio ponderado de las tres fracciones obteniendo cómo densidad de trabajo.

\[\rho = 993 [\frac{kg}{m^3}]\]

Utilizando la fórmula de Taylor para el cálculo de la viscosidad de suspensiones se obtiene:

\[\frac{\mu_{eff}}{\mu_{water}} = 1 + \frac{\mu_{water} + \frac{5}{2} \mu_{oil}}{\mu_{water} + \mu_{oil} } \theta\]

Donde:

• \(\mu_{eff}\) Viscosidad dinámica de la suspensión

• \(\mu_{water}\) Viscosidad dinámica de la fase continua.

• \(\mu_{oil}\) Viscosidad dinámica de la fase dispersa.

• \(\theta\) Proporción de la fase dispersa an la fase contínua.

\[\mu = 0.000734412 [pa s]\]

\[\nu = 7.45656e-7 [m^2/s]\]

Para la viscosidad dinámica y cinemática respectivamente.

La presión a utilizar en el modelo corresponde a 655 psi que equivalen a:

\[P = 4.516e6 [pa]\]

En los modelos de openFoam se utiliza la presión normalizada, es decir la presión dividida entre la densidad del fluido.

\[P_{*} = 4547 \frac{m^2}{s^2}\]

Por último se deben cálcular las condiciones iniciales para los parámetros \(\kappa\) y \(\epsilon\) del modelo turbulento con base en las condiciones de operación de las líneas de fluido. Para este efecto se dispone de la ecuación:

\[\nu = 0.09 \frac{\kappa^2}{\epsilon}\]

Fluido de alta presión

El fluido de alta presión es agua cuya densidad y viscosidad se suministraron por parte del cliente.

Propiedades del fluido de alta presión

Los valores a usar en el modelo son:

\[\rho = 1001.95 [\frac{kg}{m^3}]\]

\[\mu = 0.000759 [pa s]\]

\[\nu = 7.5752e-7 [m^2/s]\]

Para la densidad, viscosidad dinámica y cinemática respectivamente.

La presión a utilizar en el modelo corresponde a 2.220 psi que equivalen a:

\[P = 1.53e7 [pa]\]

La presión normalizada para openFoam es:

\[P_{*} = 15270 \frac{m^2}{s^2}\]

Malla

La malla de elementos finitos construida para el modelo se realizó mediante la extrusión de una malla bidimensional previamente mapeada de este modo la malla final resulta tambien mapeada (compuesta de hexahedros) lo que es mas eficiente que la triangularización, produce mejores mallas (menor coeficiente de no ortogonalidad) y ahorra tiempo de computo.

La figura siguiente muestra las características de la malla elaborada.

Vista frontal de la malla

Vista general de la malla

Detalles de la malla

Condiciones de frontera

El modelo realizado requiere de condiciones de frontera y condiciones iniciales consistentes para su funcionamiento. Las siguientes son las condiciones aplicadas al modelo.

Condiciones de velocidad

• Entrada del fluido: Se modela la velocidad de entrada correspondiente al máximo valor de diseño (8 \(\frac{ft}{s}\) para el fluido multifásico y 10 \(\frac{ft}{s}\) para el fluido de inyección).

• Velocidad inicial: Se modela con el mismo valor del de la entrada del fluido.

• Velocidad en las paredes: Se modela con velocidad cero en la pared (no slip).

Condiciones de presión

• Salida del fluido: Se coloca a la salida la presión máxima de trabajo.

• Entrada del fluido: Esta presión será cálculada y es el valor de salida esperado.

• Paredes: condición de zero gradiente.

• En el software utilizado (openFoam 5.x) se requiere cómo dato de presión la cantidad:

\[P*_{of}=\rho p\]

• Del mismo modo la presión obtenida debe dividirse entra la densidad para obtener el valor en unidades consistentes (\(pa\) este caso).

Condiciones de turbulencia

• Entrada salida y paredes: Se calcula valor de \(\kappa\) y \(\epsilon\) de acuerdo con las condiciones de flujo (Reynolds), y se asignan valores iniciales al modelo en la entrada, salida, pared y volumen.

Corrida y postprocesamiento

Los modelos se cargaron de acuerdo con lo indicado lineas arriba en el numeral correspondiente a las cargas y se corrieron con el software de elementos seleccionado (Ver numeral Software).

Se obtuvieron resultados de caida de presión y velocidades a través de los Slleves como se ilustra a continuación.

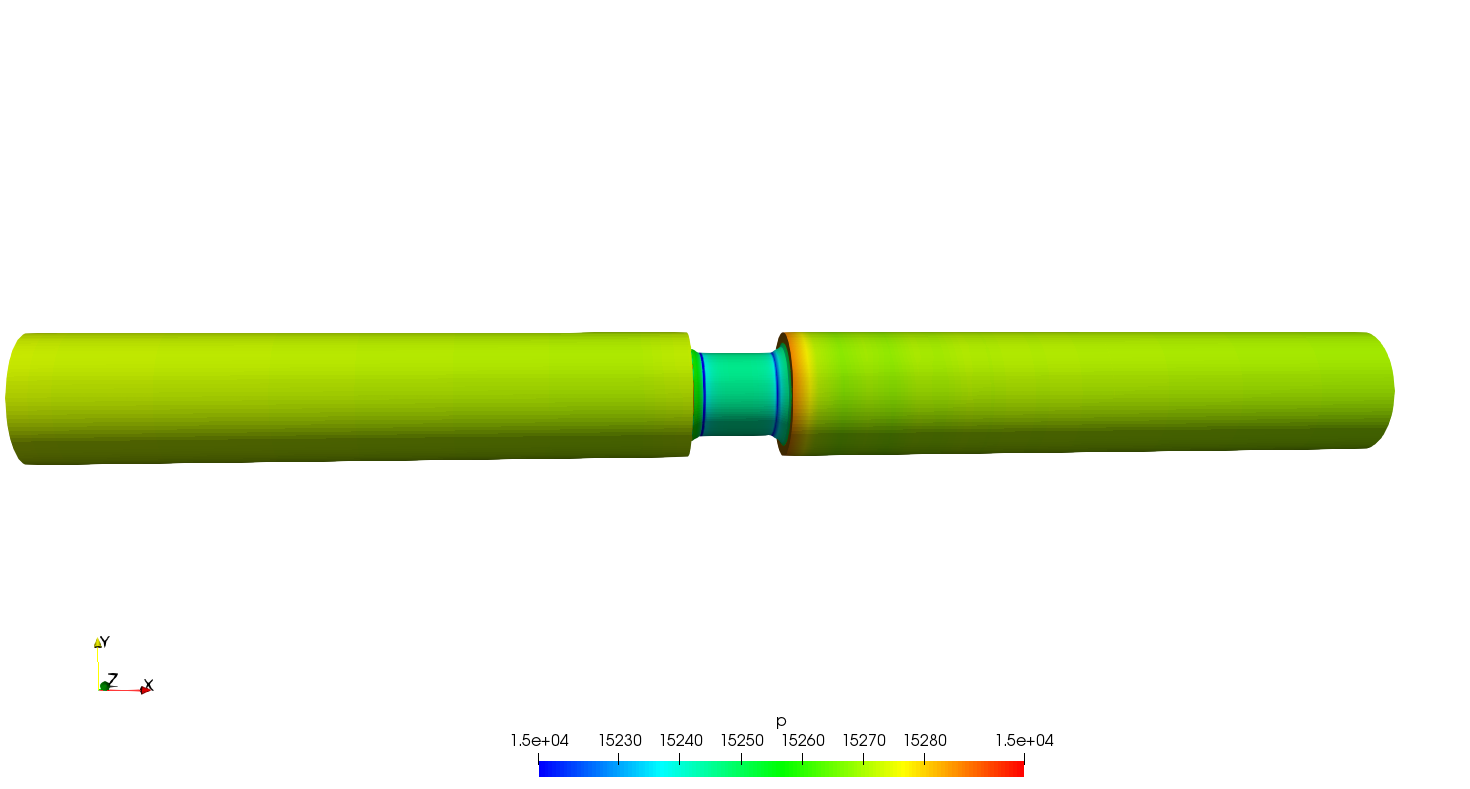
Caida de presión a través de Slleve de 3» SCH-80

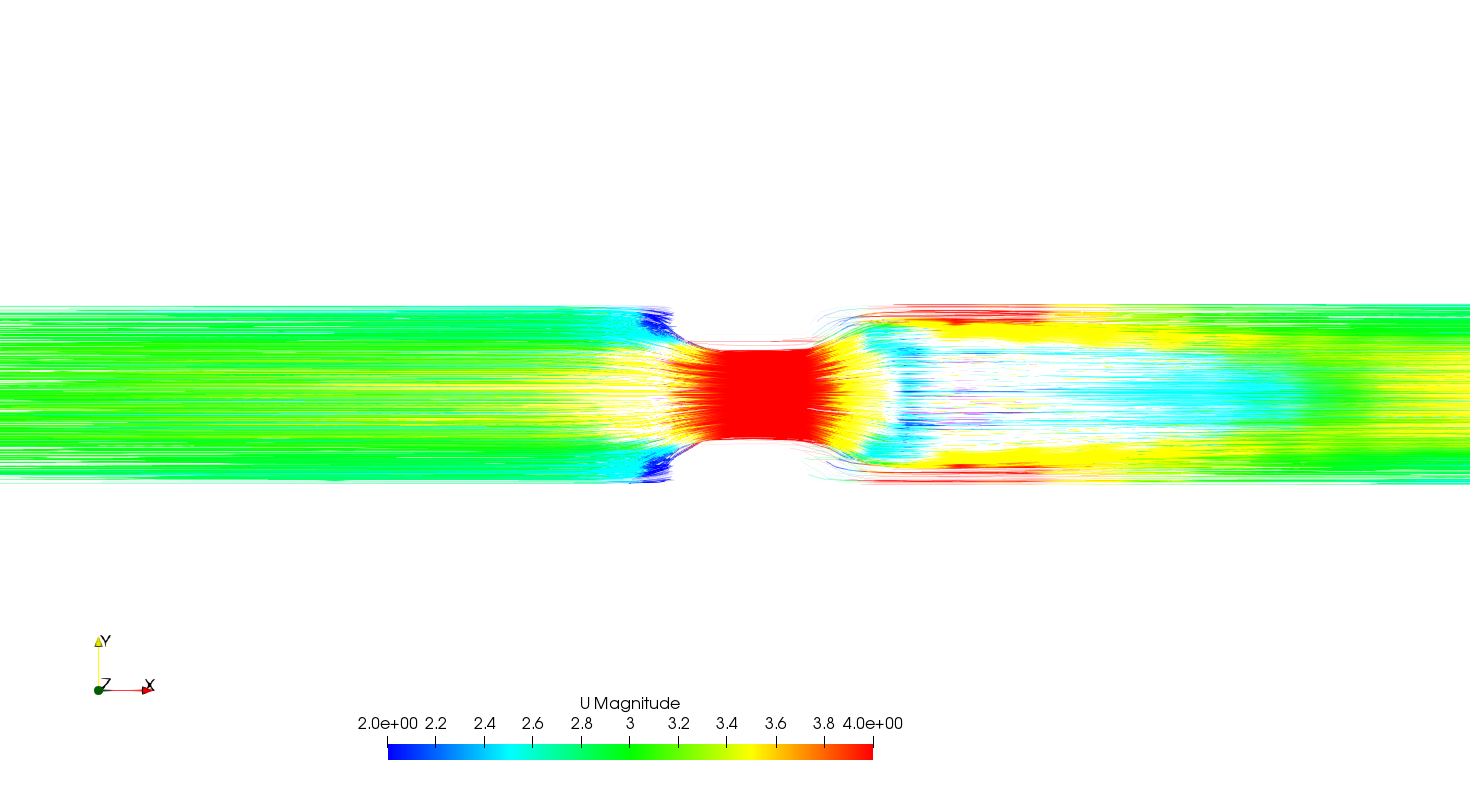
Perfil de velocidad a través de Slleve de 3» SCH-80

Software

Para la elaboración de este proyecto se utilizó el software de volúmenes finitos openFoam 5.x.

Hardware y tiempo de corrida

Para la ejecución de los modelos se utilizó un equipo con procesador Core i7 de 8va generación, 32GB Ram, con tiempos de corrida promedio de 10.000 segundos con un procesador y/o 3.000segundos con 12 procesadores.

Cálculo SCH-STD

Resultados

En la tabla siguiente se resumen los resultados obtenidos para la caida de presión enlos Slleves que utiliza actualmente el cliente.

Resultados de caida de presión en Slleves SCH-STD, a las velocidades mínima y máxima de diseño

Sllleve	Velocidad del fluido [\(\frac{ft}{s}\)]	Caida de presión [\(psi\)]
3» SCH-STD	8	0.27
	3	0.037 [4]
6» SCH-STD	8	0.128
	3	0.019 [4]
16» SCH-STD	8	0.035
	3	0.0049 [4]

[4] (1,2,3)

Este valor no se modeló, en cambio se calculó usando la relación de caudal al cuadrado para pérdidas.

Cálculo SCH-80

Resultados

Resultados de caida de presión en Slleves SCH-80, a las velocidades mínima y máxima de diseño

Sllleve	Velocidad del fluido [\(\frac{ft}{s}\)]	Caida de presión [\(psi\)]
3» SCH-80	10	0.36
	3	0.032 [5]
12» SCH-80	10	0.076
	3	0.007 [5]

[5] (1,2)

Este valor no se modeló, en cambio se calculó usando la relación de caudal al cuadrado para pérdidas.

Verificaciones

Efecto del tamaño de la malla

Se realizaron pruebas para encontrar la influencia del tamaño de la malla en el error de cálculo para la caida de presuión. Se utilizó para este efecto el modelo del Slleve de 3» SCH-STD con los siguientes resultados.

Caida de presión para diferentes tamaños de malla

Número de volúmenes	Caida de presión calculada [\(psi\)]
270.000	7.345
640000	2.160
1’250.000	0.650
2’400.000	0.27

En la figura siguiente se grafica el efecto del tamaño de la malla en la precisión del cálculo de la caida de presión. Con base en este resultado se define que el tamaño de malla para la elaboración de los modelos será cómo mínimo de 1’250.000 volúmenes finitos.

Si bien los valores del tamaño de la malla no son determinantes para la convergencia porque después del cálculo inicial se requieren algunos parámetros adicionales, la escogencia de una buena malla permitirá mejorar la precisión del cálculo.

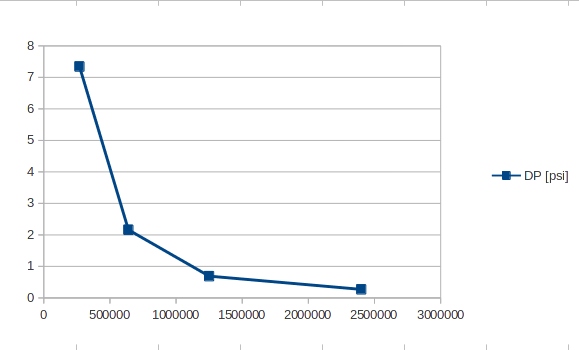
Definición del tamaño de la malla de volúmenes finitos.

Cálculo analítico

Para el cálculo analítico de las pérdidas por fricción se consideran una contracción y una expansión bruscas.

Para el sistema de agua de inyección se utiliza la relación:

\[h= \sum{K} \frac{v^2} {2 g}\]

Para el cálculo del K de perdidas para la reducción se utiliza la ecuación (2) de la bibliografía [6]

\[K_{BR} = 0.50926435 - 0.28767429 \frac{A_{2}}{A_{1}} - 1.4840581 (\frac{A_{2}}{A_{1}})^2.^5 + 1.2643591 (\frac{A_{2}}{A_{1}})^3\]

Para la expansión el K de pérdidas se calcula con la ecuación (25) de la bibliografia [6]

\[K_{AB} = 0.99906174 + 0.13856654 (\frac{A_{2}}{A_{3}})^0.^5 - 2.4035102 (\frac{A_{2}}{A_{3}}) + 1.6373483 (\frac{A_{2}}{A_{3}})^2 - 0.37144824 (\frac{A_{2}}{A_{3}})\]

Con:

\(A_{1}\) Area del tubo antes de la reducción [\(m\)] \(A_{2}\) Area del diametro interno del Slleve [\(m\)] \(A_{3}\) Area del tubo despues de la expansión [\(m\)]

Usando estas ecuaciones se realizaron los cálculos de la siguiente tabla.

Cálculo de la caida de presión mediante los coeficientes K

Sllleve	Velocidad del fluido [\(\frac{ft}{s}\)]	\(k_{BR}\)	\(k_{AB}\)	Caida de presión Calculada [\(psi\)]	Caida de presión modelada [\(psi\)]	Diferencia [%]
3» SCH-80	10	0.298	0.3161	0.41	0.36	13.8
12» SCH-80	10	0.075	0.056	0.088	0.112	21
3» SCH-STD	8	0.273	0.28	0.23	0.27	14.8
6» SCH-STD	10	0.14	0.11	0.108	0.128	15.6
16» SCH-STD	10	0.048	0.036	0.036	0.034	5.88

[6] (1,2)

Expresiones analíticas del coeficiente de pérdidas de energía en dispositivos de reducción del diámetro bajo régimen forzado, JoséJ.Villegas-León, Alvaro López-Lambraño, JoséG.Morales-Nava, Máximo Pliego-Díaz, Carlos Fuentes, Alvaro López-Ramos, 2015

Límites del análisis

• Los análisis corresponden a la solución de la ecuación de Navier Stokes para flujo estacionario.

• Los valores de caida de presión cálculados son numericamente pequeños con respecto a los valores de referencia (presiones de diseño), esto genera inestabilidades numéricas que debieron revisarse cuidadosamente para obtener convergencia.

Anexos

• Gráficas de resultados
  • Esfuerzos en Slleves actuales
• ANEXO - INTERPOLACIÓN POLINOMIAL PARA EL CÁLCULO DE K
  • Resultados