ANEXO - INTERPOLACIÓN POLINOMIAL PARA EL CÁLCULO DE K

Se realiza una interpolación polinomial a partir de los datos simulados para calcular el valor aproximnado de la constante k de pérdidas para el resto de los Slleves dentro del rango de la simulación.

Teniendo en cuenta que el ángulo de la entrada de los Slleves es el mismo en todos los casos se omite este parámetro cómo dato de entrada de la interpolación, quedando solamente cómo su dominio el diámetro interior del tubo y el diámetro interior del Slleve. Para reducir la dimensión de la interpolación se escoge cómo dominio (eje x) la relación de Areas del interior del Slleve sobre el área interior del diámetro interno del tubo. Es decir que para cada Aslleve/Atubo se tendrá un valor k de constante de pérdidas para ser usado en los cálculo hidráulicos.

import numpy as np
import matplotlib.pyplot as plt
x_pts =(0.304, 0.369, 0.578, 0.64, 0.78)
# 10 equidistant x coords from 0 to 10
y_pts =(0.7, 0.47, 0.21, 0.112, 0.089)
x_vals =(0.397, 0.4538, 0.508, 0.577, 0.616, 0.6526, 0.6914, 0.7265,
        0.73, 0.75)
# 50 desired points
y_vals =np.interp(x_vals, x_pts, y_pts)
plt.plot(x_pts, y_pts, 'o')
# plot known data points
plt.plot(x_vals, y_vals, '-x')
print(y_vals)
# plot interpolated points
plt.show()

[0.43516746 0.36450718 0.29708134 0.21124402 0.14993548 0.10993
 0.10355571 0.09778929 0.09721429 0.09392857]

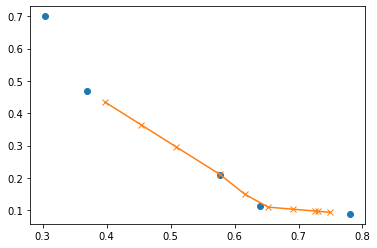
Resultados

Lospuntos en azul corresponden al cálculo realizado y los puntos amarillos son los resultados interpolados. Se observa una buena correspondencia de la interpolación lineal.